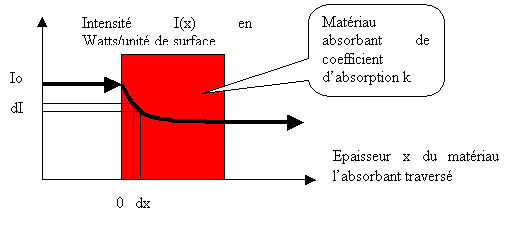
Figure 17 Absorption d'énergie par un matériau de coefficient d'absorption k
3.3. Inversion de population et différents types de pompage
3.3.1. Inversion de population
En excluant le bruit incohérent (émission spontanée), la condition de gain d'un oscillateur quantique est obtenue lorsque dN2 / dt < 0 c'est-à-dire lorsque le nombre d'atomes du niveau 2 se désexcitant diminue au cours du temps : il y a alors inversion de population). Pour cela, l'émission stimulée doit l'emporter sur l'absorption. D'après l'Equation 15 (en supprimant le terme lié à l'émission spontanée), il vient :
dN2 / dt = B12 * N1 * Rho(Nu) - B21 * N2 * Rho(Nu)
dN2 / dt = - B21 * Rho(Nu) * (N2 - N1 * B12 / B21)
dN2 / dt = - B21 * Rho(Nu) * (N2 - N1 * g2 / g1) < 0 donc :
N2 > N1 * g2 / g1
Equation 18 Condition d'inversion de population et de gain
3.3.2. Etude du coefficient d'absorption B12 dans le cas où N2 << N1
Lorsqu'un faisceau lumineux traverse une enceinte fermée contenant des atomes ou molécules absorbantes, son intensité décroît de manière exponentielle. Considérons Io l'intensité initiale du faisceau incident. Calculons la diminution dI de l'intensité I lors de la traversée d'une épaisseur dx du matériau absorbant, en fonction de l'épaisseur x :

Figure 17 Absorption d'énergie par un matériau de coefficient d'absorption k
La diminution d'intensité s'exprime par :
dI = - I * k * dx
d'où ,
dI / I = - k * dx
et par intégration, il vient :
I (x) = Io * exp(- k * x)
Equation 19 Décroissance de l'intensité lumineuse dans un matériau absorbant
Ce qui correspond bien à une décroissance exponentielle.
Notons que le coefficient d'absorption linéique k est associé à la susceptibilité électrique du matériau absorbant. Toutefois, les atomes du matériau absorbant réagissent à une certaine fréquence Nuo du rayonnement incident et la représentation k(Nu) du coefficient d'absorption linéique en fonction de la fréquence du faisceau incident Nu possède un profil Lorentzien et une largeur de raie naturelle à mi-hauteur deltaNu1/2 liée à la durée de vie de la bande d'absorption (voir 3.3.4) du matériau absorbant.
Un profil de raie Lorentzien possède la forme suivante :
k(Nu) = ko / (1 + ((Nu - Nuo) / deltaNu1/2)²)
Equation 20 Profil de raie de type Lorentzien
Avec GNUplot et en tapant la commande suivante :
gnuplot> plot [x=0:30] 10 / (1 + ((x - 15)/4)**2)
où arbitrairement, nous supposerons :
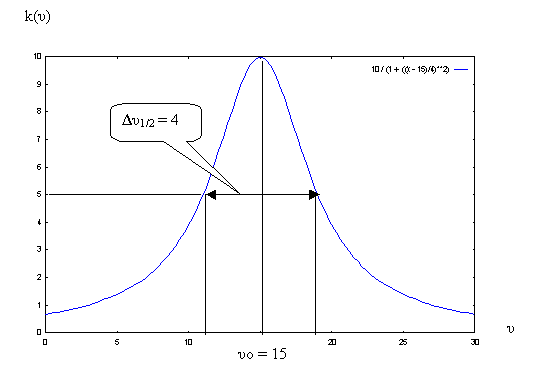
Figure 18 Profil de raie de type Lorentzien
L'aire de la Lorentzienne est donnée par intégration sur la fréquence :
Intégrale(Nu allant de - 8 à + 8) k(Nu) * dNu = (pi / 2) * deltaNu1/2 * ko
Equation 21 Aire de la Lorentzienne
Dans l'absorption précédente, nous avons supposé les atomes du matériau immobiles alors que ceux-ci sont en réalité mobiles :
Un profil de raie Gaussien possède la forme suivante :
k(Nu) = k'o * exp[- 4 * ((Nu - Nuo) / deltaNuD)² * log 2)]
Equation 22 Profil de raie de type Lorentzien
Avec GNUplot et en tapant la commande suivante :
gnuplot> plot [x=0:30] 10 * exp(- 4 * ((x - 15)/10)**2 * log(2))
où arbitrairement, nous supposerons :
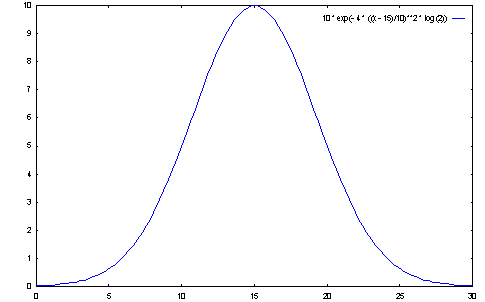
Figure 19 Profil de raie de type Gaussien
Comparons maintenant les deux profils pour voir l'élargissement Doppler. Pour cela, il suffit de taper la commande suivante :
gnuplot> plot [x=0:30] 10 * exp(- 4 * ((x - 15)/10)**2 * log(2)), 10 / (1 + ((x - 15)/4)**2)
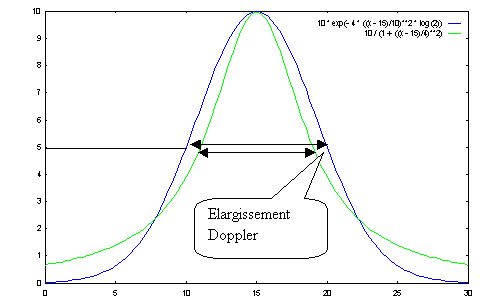
Figure 20 Elargissement Doppler d'un profil de raie
Dans le cas d'un matériau absorbant de type Néon, la longueur d'onde du faisceau LASER est de 6328 Angströms et les largeurs de raie sont :
Le gain du milieu actif constituant le LASER dépend également de la fréquence qui le traverse. La courbe du gain en fonction de la fréquence g(Nu) est de type gaussienne, de largeur à mi-hauteur deltaNu.
Le paramètre deltaNu est d'autant plus grand que le désordre du système cristallin (plus un tel système est désordonné, plus il possède de modes de vibration).
3.3.3. Différents types de pompages
Les interactions ont un rôle primordial dans l'obtention d'une inversion de population (N2 > N1). Selon les particules composant le milieu actif, le pompage nécessaire à cette inversion, ne sera pas le même :
3.3.4. Exemples de pompages optiques
3.3.4.1. LASER à 3 niveaux
En 1960, Maiman travaillait sur des LASERs à rubis dopé aux ions chrome Cr3+. Les atomes du rubis dopé pouvait se trouver dans 3 états d'énergie E1 (état fondamental des dopants Cr3+), E2 (état intermédiaire dans lequel l'atome ne reste qu'un instant très bref) et E3 (état excité).
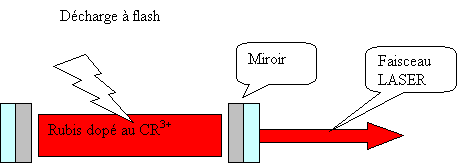
Figure 21 LASER à rubis de Maiman
Comme tout système à plusieurs états, une transition d'un état à un autre est associée à un phénomène physique :
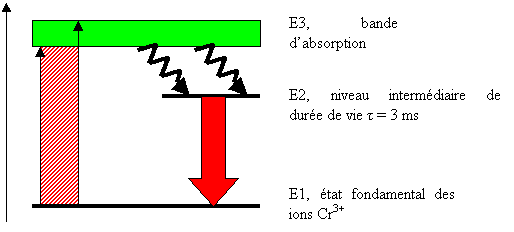
Figure 22 LASER à 3 niveaux d'énergie
L'inconvénient d'un tel LASER est d'utiliser le niveau d'énergie fondamental, ce qui a pour conséquence de faire fonctionner le LASER en mode pulsé. Toutefois, ce type de LASER a trouvé une application pour les communications optiques longue distances telles que celles utilisées pour former la " toile infrarouge Internet " avec un milieu actif dopé aux ions erbium Er3+ et une émission à la longueur d'onde 1.55 µm et un pompage optique de 0.980 µm. De tels LASERs permettent de réamplifier le signal au niveau des répéteurs placés tous les 100 km de fibres optiques. Aujourd'hui, le flash permettant le pompage optique, et l'inversion de population, est fourni par un LASER à semi-conducteur.
3.3.4.2. LASER à 4 niveaux
Dans ce type de LASER, un cristal YAG (Yttrium Aluminium Grenat) est dopé avec des ions Néodyme Nd3+. Ce LASER est connu pour son caractère dangereux pour la vue : en effet, il émet dans le domaine de l'infrarouge qui est absorbé et détériore l'il sans que ce dernier ne s'en rende compte.
Dans ce LASER à 4 états, les transitions sont les suivantes :
Notons que comme l'écart énergétique entre les niveaux E1 et E2 est très grand devant le produit k * T (Constante de Boltzmann * Température) si bien que le nombre d'atomes occupant le niveau 2 est quasi nul d'après la distribution de Boltzmann et l'inversion de population entre les niveaux E2 et E3 s'en trouve plus aisée.
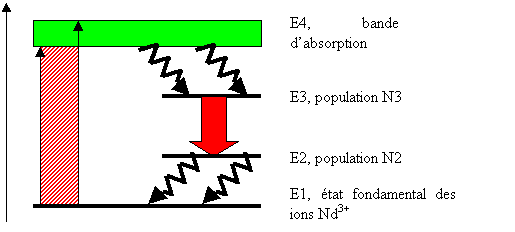
Figure 23 LASER à 4 niveaux d'énergie
3.3.4.3. LASER à colorant à 4 niveaux
Les LASERs à colorant de type Rhodamine R6G possèdent une bande d'absorption E2 beaucoup plus large que les LASERs à 4 niveaux précédents. La bande de fluorescence étant plus large, ce LASER émet dans une gamme de longueurs d'onde dans le domaine du visible. Ce LASER est accordable et il est possible de sélectionner une longueur d'onde particulière à l'aide d'un réseau à prisme. Il est utilisé en photothérapie du cancer à la longueur d'onde de 6300 Angströms.
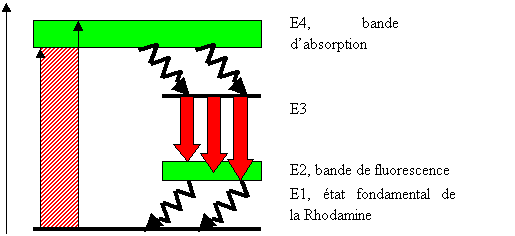
Figure 24 LASER à colorant à 4 niveaux d'énergie
3.3.4.4. LASER à 5 niveaux
Dans ce type de LASERs, trois niveaux d'énergie sont utilisés pour le pompage optique et deux niveaux le sont pour l'effet LASER (oscillation). De tels LASERs utilisent les ions Nd3+ et sont également appelés LASER à " up conversion ". Le pompage optique se fait par absorption de deux photons successifs, d'où l'introduction du 5ème niveau d'énergie car l'énergie des photons de pompage h * Nu (pompage - rouge) est inférieure à l'énergie des photons du faisceau LASER h * Nu (LASER - bleu). Physiquement, en éclairant des ions Nd3+ à l'aide d'un faisceau de pompage rouge, un faisceau bleu est obtenu en sortie du LASER. Notons que le pompage optique est réalisé à l'aide d'un autre LASER.
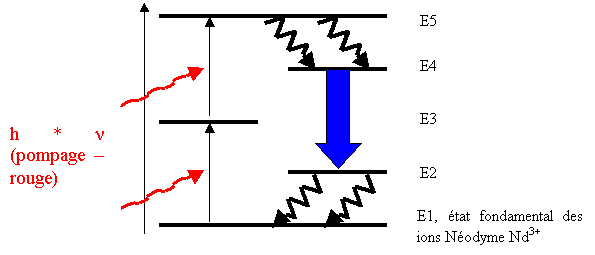
Figure 25 LASER à 5 niveaux
3.3.5. Exemples de pompages électriques
Le pompage électrique consiste à bombarder les atomes du milieu actif du LASER par des électrons. Plusieurs LASERs utilisent un tel type de pompage :
Dans le cas des systèmes He-Ne étudiés par Javan en 1960, des atomes d'Hélium He et de Néon Ne sont placés dans une enceinte fermée (capsule de verre) comportant une anode A et une cathode K à chaque extrémité. Une différence de potentiels (d.d.p.) étant appliquée entre l'anode et la cathode, des électrons circulent dans l'enceinte et bombardent les atomes He et Ne. En effet, un champ électrique E s'établit de l'anode vers la cathode si le potentiel positif est relié à l'anode et si le potentiel négatif est relié à la cathode. La force électrique coulombienne due à la charge négative de l'électron entraîne alors ce dernier dans le sens opposé (F = charge * E = - e * E avec e, la charge élémentaire 1.6 * 10-19 Coulombs). Lors des collisions électron-atome, l'énergie cinétique des électrons (obtenue par accélération entre la cathode et l'anode) :
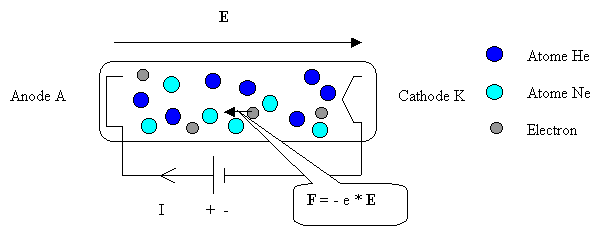
Figure 26 Système He-Ne de Javan (1960)
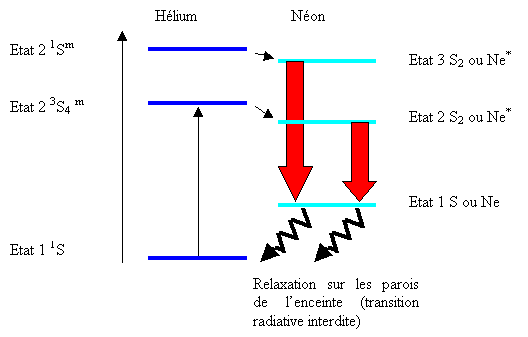
Figure 27 Système He-Ne