4.1. Etude du milieu actif des LASERs à SC

4.1.1. SC à gap direct et indirect

Elaborés en 1962 en régime pulsé puis en régime continu, les LASERs à SC fonctionnent dans toutes les gammes de longueur d'onde allant de 0.4 à 30 µm et sont utilisés comme LASERs de pompe (pompage optique) ou de lecture.

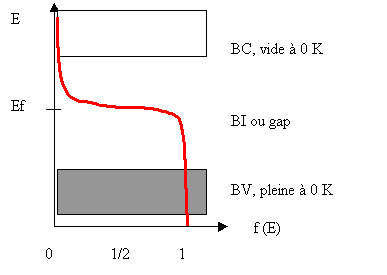
Les SC sont caractérisés par les états énergétiques des électrons les composants. En effet, les électrons peuvent occuper l'une ou l'autre des bandes d'énergie suivantes :

• · La bande de valence (BV) pleine à la température de 0 K
• · La bande de conduction (BC) vide à la température de 0 K

Entre les deux, se trouve la bande interdite (BI ou gap) au milieu de laquelle se trouve le niveau énergétique de Fermi Ef.

Lorsque le SC se trouve à l'équilibre thermodynamique, la répartition des électrons du solide dans les bandes d'énergie est décrite par la statistique de Fermi-Dirac. A l'équilibre thermodynamique , la probabilité de trouver un électron d'énergie vaut :

f(E) = 1 / (1 + exp(Beta * (E - Ef)))

Equation 23 répartition énergétique des électrons d'un SC

Avec :

• · Beta = 1 / (k * T)
• · k * T = l'énergie thermique
• · Ef = le niveau de Fermi tel que f(Ef) = 1/2

Dans le cas d'un SC intrinsèque (pur c'est-à-dire non dopé), les électrons sont liés donc lorsque la température diminue, le nombre d'électrons passant de la BV à la BC diminue ainsi que la conductivité du matériau. Si bien que la résistivité du SC augmente. A température ambiante (290 K), la résistivité du SC est comprise entre 10-2 et 109 Ohm.cm.

Le schéma des bandes de valence et de conduction est le suivant :

Figure 28 Bandes de valence et de conduction d'un SC

Le principe d'exclusion de Pauli interdit à la fonction f(E) de prendre toute valeur supérieure à 1. Pour une température T non nulle, la conductivité intrinsèque du SC augmente et la bande de conduction commence à se remplir. Cette transition de l'électron de la BV vers la BC peut se faire par absorption d'un photon. Pour que cette transition ait lieu, il faut qu'il y ait conservation de l'énergie E et du vecteur d'onde k. Deux cas sont à considérer :

• · SC à gap direct : seule l'énergie varie, pas le vecteur d'onde (valable pour les alliage de type III-V avec les éléments des colonnes III et V du tableau périodique des éléments de Mendeleïev : GaAS, Ga1-xAlxAs, Ga1-xAlxAs1-yPy et InP).
• · SC à gap indirect : l'énergie et le vecteur d'onde varient (valable pour les éléments de la colonne IV du tableau périodique des éléments : Si et Ge).

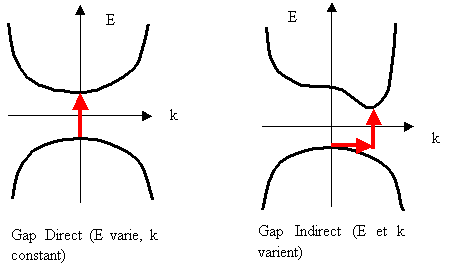
Figure 29 Gap direct et gap indirect d'un SC

Si la longueur d'onde du photon autorisant la transition électronique est de 10000 Angströms alors le vecteur d'onde du photon est égal à 2 * pi / 10000 Angströms. De plus, dans le cas d'une transition indirecte (gap indirect), le vecteur d'onde du phonon est égal à 2 * pi / 5 Angströms, ce qui est très supérieur au vecteur d'onde du photon. Nous en déduisons que le phonon absorbe toute l'énergie dans le cas d'un gap indirect et que l'effet LASER n'a pas lieu.

Bilan :

Les LASERs à SC ne sont pas conçus à partir de Si ou Ge (gap direct) mais à partir d'alliage de type III-V ou II-VI (gap indirect).

4.1.2. Dopage des SC à gap direct

Le dopage des SC à gap indirect permet de réduire ou augmenter la résistivité Rho du milieu et de modifier le niveau de Fermi. La concentration en atomes " dopants " est de l'ordre de 108 atomes / cm3 et la longueur d'onde d'émission LASER correspond aux domaines :

• · Du visible et de l'infrarouge pour les SC de la famille III-V
• · Du bleu à l'Ultraviolet pour les SC de la famille II-VI

Extrait du tableau de Mendeleïev:

II	III	IV	V	VI
	Al	Si	P
Zn	Ga	Ge	As	Se
Cd	In	Sn	Sb	Te
	Tl	Pb	Bi

Accepteurs d'électrons (dopants de type p): colonnes II et III

Donneurs d'électrons (dopants de type n): colonnes V et VI

Table 1 Extrait du tableau de Mendeleïev

Dans le cas d'un SC fortement dopé, le niveau de Fermi se décale :

• · Dans la BC (Ef augmente) pour un dopage de type n ;
• · Dans la BV (Ef diminue) pour un dopage de type p.

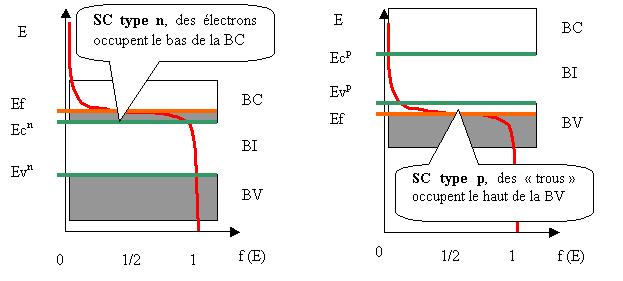
Figure 30 Bandes d'énergie d'un SC dopé de type n ou p

4.1.3. Jonction p-n pour GaAs fortement dopé et effet LASER

Etudions l'interface entre deux SC fortement dopés de type n et p : une telle structure s'appelle jonction p-n (et se retrouve dans les diodes en électronique). Le SC considéré est le GaAs (famille III-V). A l' équilibre, les niveaux d'énergie ne sont pas excités et les niveaux de Fermi des deux SC s'alignent.

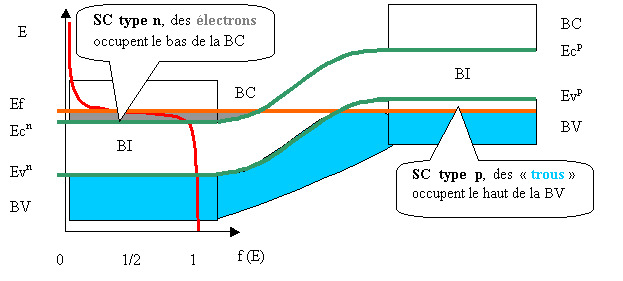
Figure 31 Jonction p-n à l'équilibre (pas de courant, I = 0)

Pour placer cette jonction hors équilibre, il suffit d'appliquer un potentiel positif au SC de type p et un potentiel négatif au SC de type n (polarisation directe). La d.d.p. en résultant crée un champs magnétique E (orienté dans le sens des potentiels décroissants) qui décale les niveaux de Fermi (qui deviennent des " quasi niveaux de Fermi "). Si bien que les électrons du SC de type n sont attirés vers les trous du SC de type p avec lesquels ils se recombinent. Le flux d'électrons se caractérise par un courant I non nul dans le sens inverse. Notons que les électrons ont été injectés dans la zone de type n par la pile à l'origine de la d.d.p.. Si les potentiels sont appliqués aux autres extrémités de la jonction p-n (polarisation inverse), il ne se passe rien (à par un décalage des niveaux de Fermi). Une jonction p-n ne laisse donc passer le courant électrique que dans un sens et c'est la raison pour laquelle elles sont utilisées dans les diodes utilisées en électronique.

Seulement la jonction p-n considérée est établie à l'aide de GaAs et la recombinaison électron-trou correspond à une désexcitation des électrons du niveau E2 vers le niveau E1. cette désexcitation s'accompagne de l'émission d'un photon de longueur d'onde 0.86 µm : il y a effet LASER.

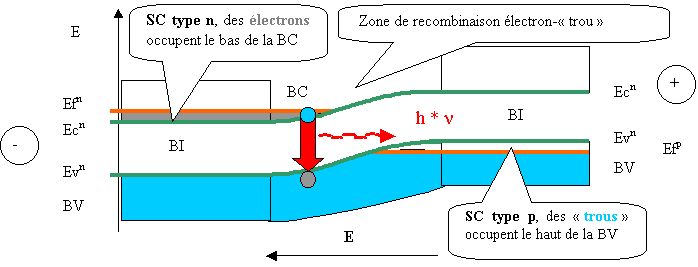
Figure 32 Jonction p-n hors équilibre (courant I non nul et déplacement d'électrons)

Bilan :

• · Les électrons et les trous diffusent dans la jonction p-n et le niveau de Fermi se dédouble en deux " quasi niveaux " Efp et Efn. Le système est alors hors équilibre (Shockley).
• · Un gain lumineux (effet LASER) est possible à l'interface de la jonction où coexistent les électrons et les " trous " (absence d'électron) : il y inversion de population.
• · Le gain du SC a été obtenu par polarisation, c'est-à-dire par injection directe d'électrons dans la BC.
• · Il existe une autre méthode d'obtention de gain dans un SC : le pompage optique mais cette solution n'est pas utilisée.

4.1.4. Oscillation dans une cavité SC composé de GaAs

Considérons la jonction p-n précédente hors équilibre, formant une diode LASER. Les semi-conducteurs de type n et p sont à base de GaAs d'indice de réfraction n = 3.5. Etant placé dans l'air, d'indice de réfraction n = 1, les miroirs sont inutiles car le faisceau LASER émis par le milieu actif (zone de recombinaison électron-" trou ") est réfléchi par les parois du cristal de SC de par les différences d'indice (voir les lois optiques de la réflexion de Snell-Descartes).

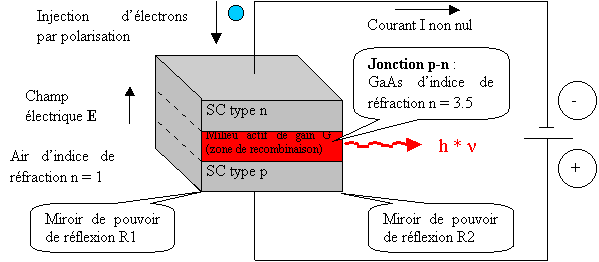
Figure 33 Diode LASER à base de SC

Les parois réfléchissantes du SC permettent l'oscillation. La condition d'oscillation est G * R = 1 avec R = ((n - 1)/(n + 1))² = 0.3 donc le gain est de l'ordre de 3. Le courant de polarisation minimum pour obtenir une oscillation est de l'ordre de 50000 Ampères par cm² de milieu actif du SC dans le cas d'une jonction p-n simple. Ce courant est phénoménal et c'est la raison pour laquelle en 1963, les premiers LASERs à SC fonctionnaient en régime pulsé.