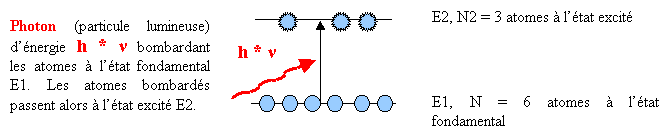
Figure 7 Système à deux niveaux d'énergie absorbant un photon
3.2. Corps noir et interaction matière-rayonnement
3.2.1. Statistique de Boltzmann
En 1872, l'Autrichien Boltzmann, connus par ses travaux d'interprétation de la notion d'entropie, fonde la théorie statistique qui porte son nom. Dans cette statistique, considérons N particules discernables n'interagissant pas entre elles. Plaçons-les à l'équilibre thermodynamique et chaque niveau d'énergie Ei est occupé par Ni particules tel que :
Ni (équilibre thermodynamique) = (N * gi * exp (- Beta * Ei)) / (Sommei gi * exp (- Beta * Ei))
Equation 3 Statistique de Boltzmann
Avec :
Dans le cas d'un système à deux niveaux d'énergie E1 et E2, et dans le cas d'une même dégénérescence (g1 = g2), nous obtenons la distribution de Boltzmann (Equation 1) :

Figure 7 Système à deux niveaux d'énergie absorbant un photon
D'après la statistique de Boltzmann, le rapport des populations des deux niveaux d'énergie est :
N2 / N1 = (g2 / g1) * exp (- Beta * (E2 - E1)) d'après l'Equation 3
Comme g1 = g2, il vient :
N2 / N1 = exp (- Beta * (E2 - E1)) (Equation 1)
Et comme l'énergie du photon est précisément égale à l'écart énergétique entre les deux niveaux, le photon est absorbé par le système contenant les N particules. Il est plus particulièrement absorbé par les atomes se trouvant dans l'état fondamental. Après absorption, ces atomes passent à l'état excité et dépeuplent le niveau inférieur pour peupler le niveau supérieur.
L'équation précédente devient, en prenant en compte l'énergie du photon h * Nu = E2 -E1 :
N2 / N1 = exp (- Beta * (E2 - E1)) = exp ( -(h * Nu) / (k * T))
Equation 4 Système à deux niveaux et absorption d'un photon
Avec :
3.2.2. Statistique de Fermi-Dirac
Dans cette statistique, les particules considérées s'appellent des " fermions " et possèdent un " spin " semi-entier. Si nous considérons un système composé de N fermions indiscernables, ceux-ci doivent obéir au Principe d'exclusion de Pauli. A l'équilibre thermodynamique, le nombre de fermions Ni peuplant le niveau d'énergie Ei est :
Ni (équilibre thermodynamique) = gi / (B * exp (+ Beta * Ei) + 1)
Equation 5 Statistique de Fermi-Dirac
Avec :
· B tel que Sommei Ni(équilibre thermodynamique) = N, une constante de normalisation
3.2.3. Statistique de Bose-Einstein
Dans cette statistique, les particules considérées s'appellent des " bosons " et possèdent un " spin " entier. Un système composé de N bosons indiscernables est sans contrainte d'exclusion contrairement à un système composé de N fermions indiscernables.
3.2.4. Lois du corps noir : Wien et Rayleigh-Jeans
Vous avez déjà remarqué qu'en appliquant n'importe quelle lumière sur une surface noire, celle-ci n'était pas réfléchie mais totalement absorbée. En 1859, Kirchhoff imagine un corps absorbant intégralement toutes les radiations qu'il reçoit (en particulier les radiations lumineuses). Il nomme alors ce corps " corps noir ".
A la fin du XIXème siècle, les physiciens étudient le rayonnement d'un corps noir isolé de l'extérieur absorbant lui-même l'énergie qu'il émet :

Figure 8 Rayonnement du Corps Noir
Ce corps noir est porté à la température T et la cavité créée en son cœur possède un volume V. A l'aide des lois de la thermodynamique, l'Autrichien Stefan montre que l'énergie émise par le corps noir est proportionnelle à la puissance quatrième de la température. Cette relation est plus connue sous le nom de " loi de Stefan ".
Ensuite, Wien indique comment passer de la répartition spectrale de cette énergie Rho (Nu) à une température donnée à celle obtenue pour une autre température. La courbe représentant l'énergie émise en fonction de la longueur d'onde possède une forme de cloche à une température donnée. Lorsque la température diminue, l'énergie maximale associée au sommet de cette courbe diminue alors que la longueur d'onde maximale Lambdamax associée à ce même sommet augmente. Ce phénomène est connu sous le nom de " loi de déplacement de Wien " :
Lambdamax * T = 2900 µm * K
Equation 6 Loi de déplacement de Wien
Avec : · Lambda, la longueur d'onde émise par le corps noir · T, la température du corps noir
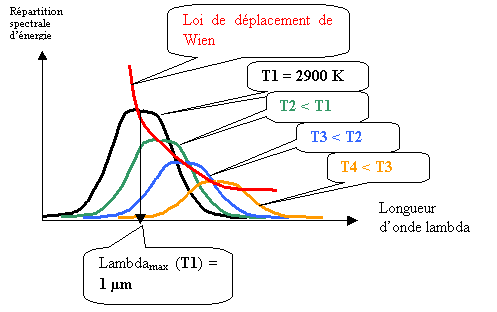
Figure 9 Répartition spectrale d'énergie de Wien
Pour ramener ce phénomène physique à des notions plus réalistes, notons que tout corps porté à une température T rayonne électromagnétiquement, tout comme le corps noir, dans une bande spectrale dépendant de la température T. Par exemple, le corps humain, de température T = 209 K rayonne à la longueur d'onde lambdamax = 10 µm et c'est la raison pour laquelle sa présence est détectable par une caméra sensible aux rayonnements infrarouge.
Lorsque la température d'un corps incandescent augmente, la couleur du corps vire au blanc puis vers le bleu mais le matériau fond avant de l'avoir atteinte (le matériau se " sublime "). Dans le cas du filament d'une lampe à incandescence (l'ampoule domestique), le Tungstène est utilisé car ce métal possède la température de fusion la plus élevée (de l'ordre de 3600 K). En 1879, Edison chauffe un filament de Tungstène à 2800 K, ce qui le fait rayonner à 90 % dans l'infrarouge et à 10 % dans le blanc. Toutefois, les lampes à incandescence ne peuvent être utilisées plus de 1000 heures contrairement aux lampes à quartz-halogène pour lesquelles la température de chauffage du filament et la durée de vie sont supérieures.
Malheureusement, la répartition spectrale d'énergie de Wien n'est vérifiée dans la pratique que pour la partie des courbe située en dessous de la courbe rouge associée à la loi de déplacement de Wien. Au-dessus de cette dernière, la théorie n'est plus vérifiée dans la pratique et la thermodynamique s'est montrée impuissante à préciser davantage cette répartition spectrale d'énergie.
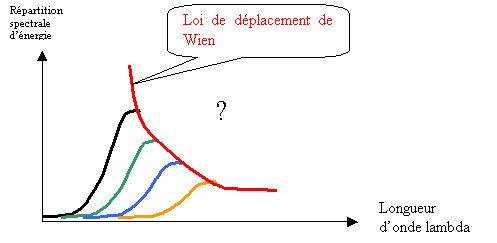
Figure 10 Répartition spectrale d'énergie de Wien non vérifiée au deus de la loi de déplacement
A la fin du XIXème siècle, l'Anglais Rayleigh s'appuie sur les hypothèses atomiques et électroniques récentes pour établir la formule gouvernant la partie inconnue de la courbe précédente (Figure 10). Malheureusement, sa formule était contraire à l'expérience pour de petites longueurs d'onde mais valable toutefois pour de grandes longueurs d'onde. Cette formule dit qu'à l'intérieur d'une cavité portée à la température T (le corps noir possède une cavité), s'établissent un certain nombre de modes d'oscillation par unité de volume et de fréquence, noté :
m (Nu) = 8 * pi * Nu² / c3
Equation 7 Nombre de modes d'oscillation d'une cavité résonnante par unité de volume et de fréquence
Avec : · Nu, la fréquence · c, la vitesse de la lumière (environ 300 000 km par seconde)
Imaginons cette cavité comme le chevalet et le sillet d'une guitare entre lesquels vibre une corde. Les modes d'oscillation constituent la note fondamentale et les harmoniques.
A la fin de ce siècle, il fallait combiner les répartitions spectrales d'énergie de Wien (pour les faibles longueurs d'onde) et de Rayleigh-Jeans (pour les longueurs d'onde élevées) pour expliquer l'expérience. Cette combinaison est appelée " Loi du corps noir ". L'introduction des " quanta " allait révolutionner ces deux théories classiques au début du vingtième siècle.
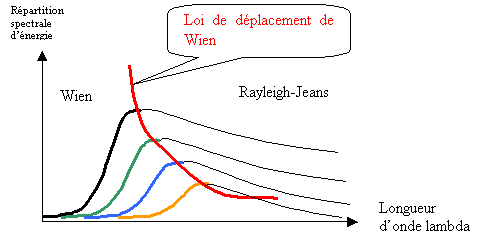
Figure 11 Loi du corps noir
3.2.5. Hypothèse de Planck
A la fin du XIXème siècle, les théories classiques tentant d'expliquer le rayonnement du corps noir aboutissent aux lois de Wien et Rayleigh-Jeans. Seulement ces lois ne faisaient qu'approcher l'expérience.
En 1900, l'Allemand Max Planck décide de modifier ces théories classiques en rejetant la continuité des deux lois classiques au niveau de la courbe correspondant à la loi de déplacement de Wien (Figure 11). En effet, Planck pose le postulat que " la matière ne peut émettre l'énergie que d'une manière discontinue, par quantités finies, appelées quanta, dont la valeur est proportionnelle à la fréquence ". Ce postulat a donné lieu à la " loi de Planck " :
deltaE = h * Nu
Equation 8 Loi de Planck
Avec : · deltaE une variation d'énergie correspondant à la quantité émise par la matière · h, constante de Planck, h = 6.63 * 10-34 Joules * secondes. · Nu, fréquence du photon émis par la matière
En se basant sur ce postulat, Planck étudie à son tour le corps noir et parvient en 1909 à établir la loi expérimentale régissant le rayonnement du corps noir. La loi trouvée coïncide avec les expériences.
L'hypothèse de Planck de 1909 est la suivante :
· Boltzmann, dans sa statistique, considère des molécules discernable (contenu quantifié) placées dans une enceinte fermée (contenant continu)
· Planck analyse le système de façon inverse au sens où il considère l'énergie émise par le corps noir, de répartition spectrale d'énergie Rho (Nu) (contenu continu), se " plaçant " selon des modes d'oscillation de Rayleigh (contenant quantifié).
Pour une fréquence Nu de Rho (Nu) donnée, l'énergie des modes est quantifiée et peut être égale à un nombre entier de quanta (d'après la loi de Planck) . Le contenu (l'énergie) devient :
E = n * h * Nu pour Nu donnée.
L'énergie moyenne d'un mode est donnée par la statistique de Boltzmann et s'exprime par :
En 1924, Bose retrouvera cette formule en assimilant les photons et les bosons.
Pour une fréquence Nu donnée, la densité de modes ou répartition spectrale d'énergie, est égale au nombre de modes par unité
de volume et de fréquence que multiplie l'énergie moyenne d'un mode :
Rho (Nu) = m (Nu) * Equation 9 Densité spectrale d'énergie de Planck
Or, comme Rho (Nu) * dNu = Rho (Lambda) * dLambda,
alors Rho (Lambda) = Rho (Nu) * | dLambda / dNu | = Rho (Nu) * c / Lambda²
et nous obtenons la loi du corps noir :
Rho (Lambda ; T) = ((8 * pi * h * c) / Lambda5) * 1 / (exp (+ h * c / (Lambda * k * T)) - 1)
Equation 10 Loi du corps noir de Planck
En prenant les valeurs suivantes :
· h = 6.63 * 10-34 J * s
· c = 3 * 108 m / s
· k = 1.38 * 10-23 J / K
Il vient :
Rho (Lambda[µm] ; T) = 8 * pi * 3 * 6.63 * 104 / (Lambda[µm]5 * (exp(6.63 * 3 / (Lambda[µm] * 1.38 * 10-3 * T)) - 1))
En utilisant GNUplot et en tapant la commande :
gnuplot> splot [x=0:10] [y=0:2900] 8 * pi * 3 * 6.63 * 10**4 / (x**5 * (exp(6.633 / (x * 1.38 * 10**-3 * y)) - 1))
Nous obtenons le courbe suivante :
Et pour les températures T = 300 K (corps humain, LASER à He-Ne, LASER à semi-conducteur), 600 K et 900 K (LASER à Ar+),
avec une longueur d'onde variant de 0 à 30 µm, il vient :
gnuplot> plot [x=0:30] 8 * pi * 3 * 6.63 * 10**4 / (x**5 * (exp(6.63* 3 / (x * 1.38 * 10**-3 * 300)) - 1)),
8 * pi * 3 * 6.63 * 10**4 / (x**5 * (exp(6.63* 3 / (x *1.38 * 10**-3 * 600)) - 1)),
8 * pi * 3 * 6.63 * 10**4 / (x**5 * (exp(6.63 * 3 / (x *1.38 * 10**-3 * 900)) - 1))
Bilan sur la loi du corps noir :
3.2.6. Transitions et processus radiatifs 3.2.6.1. Absorption Un atome peut se trouver dans plusieurs états d'énergie discrets. Pour transiter d'un état d'énergie E1 à un état d'énergie E2 > E1, l'atome
doit absorber un photon d'énergie h * Nu égale à E2 - E1. L'absorption est le premier des processus transitoires cohérent car les photons non absorbés
conservent la même fréquence, la même phase, la même polarisation et la même direction que les photons incidents. Pour cette raison, l'absorption est
également appelée soustraction cohérente.
L'absorption est proportionnelle au nombre N1 d'atomes dans l'état 1 et à la densité spectrale d'énergie Rho (Nu). La probabilité de
transition par absorption du niveau 1 au niveau 2 est B12. Le nombre dN1 d'atomes du niveau 1 absorbant un photon pendant un intervalle de temps dt est :
dN1 = - B12 * N1 * Rho (Nu) * dt
Equation 11 Absorption pendant dt
3.2.6.2. Emission stimulée Une fois dans son état excité, l'atome peut retourner dans l'état fondamental en émettant un photon suite au bombardement par un photon
incident. La désexcitation de l'atome est " stimulée " par le photon incident. Ce processus est dit " radiatif " car il y a émission d'un photon et s'appelle
émission stimulée ou induite. Ce processus est intimement lié à l'absorption et est appelé addition cohérente (pour la même raison que l'absorption est
appelée soustraction cohérente).
L'émission stimulée est proportionnelle au nombre N2 d'atomes dans l'état 2 et à la densité spectrale d'énergie Rho (Nu). La probabilité
de transition par émission stimulée du niveau 2 au niveau 1 est B21. Le nombre dN2 d'atomes du niveau 2 émettant un photon par émission stimulée
pendant un intervalle de temps dt est :
dN2 = - B21 * N2 * Rho (Nu) * dt
Equation 12 Emission stimulée pendant dt
Les processus d'émission stimulée et d'absorption étant liés, il vient :
dN2 = - dN1
3.2.6.3. Emission spontanée Contrairement à l'émission stimulée où l'atome dans l'état 2 est bombardé par un photon incident (stimulus) avant de se désintégrer,
ce même atome se désintègre spontanément et sans stimulus dans l'émission spontanée.
L'émission spontanée est proportionnelle au nombre N2 d'atomes dans l'état 2 et est indépendante de la densité spectrale d'énergie Rho(Nu)
car il n'y a pas d'interaction entre un rayonnement externe (photons incidents) et les atomes. Le photon émis l'est de manière quelconque en terme de phase,
polarisation et direction. La probabilité de transition par émission spontanée du niveau 2 au niveau 1 est A21. Le nombre dN2 d'atomes du niveau 2 émettant
un photon par émission spontanée pendant un intervalle de temps dt est :
dN2 = - A21 * N2 * dt
Equation 13 Emission spontanée pendant dt
La durée de vie du niveau 2 s'en déduit :
dN2 / N2 = - A21 dt donne par intégration ln N2 = - A21 * t soit N2 (t) = exp (- A21 * t)
que nous pouvons réécrire N2 (t) = exp (- t / Dvie)
avec Dvie la durée de vie du niveau 2.
Dvie = 1 / A21
Equation 14 Durée de vie du niveau 2
3.2.7. Rapport A/B d'Einstein En 1917, Einstein compare, à l'équilibre thermodynamique, le rayonnement émis par un système à deux niveaux et celui d'un corps noir
de densité spectrale d'énergie Rho(Nu). En nous concentrant sur l'évolution du nombre d'atomes peuplant le niveau 2 en fonction du temps, il vient pour
les trois processus transitoires précédents :
dN2 / dt = (dN2 / dt)spt + (dN2 / dt)abs + (dN2 / dt)stm
dN2 / dt = - A21 * N2 + B12 * N1 * Rho(Nu) - B21 * N2 * Rho(Nu)
Equation 15 Evolution du nombre d'atomes se désexcitant par émission d'un photon
A l'équilibre thermodynamique, dN2 / dt est nulle donc :
N2 / N1 = B12 * Rho(Nu) / (A21 + B21 * Rho(Nu)) = (g2 / g1) exp(- h * Nu / (k * T)) d'après la distribution de Boltzmann
Ou bien,
Rho(Nu) = A21 / (B12 * (N1 / N2) - B21)
La première expression N2 / N1 est valable pour toutes les températures. Supposons cette température extrêmement élevée et dans
ce cas la densité spectrale d'énergie l'est également (le corps noir devient extrêmement brillant). Si T et Rho(Nu) tendent vers l'infini alors :
N2 / N1 # B12 / B21 # g2 / g1 (le signe " # " signifie " proche de ")
La seconde expression Rho(Nu) devient alors :
Rho(Nu) = A21 / ((g2 / g1) * B21 * (N1 / N2) - B21), soit :
Rho(Nu) = A21 / (((g2 / g1) * (N1 / N2) - 1) * B21), et en tenant compte de la première expression de N2 / N1 ramenée à N1 / N2:
Rho(Nu) = A21 / (((g2 / g1) * (g1 / g2) exp(+ h * Nu / (k * T)) - 1) * B21)
En simplifiant, il vient :
Rho(Nu) = A21 / ((exp(h * Nu / (k * T)) - 1) * B21)
Equation 16 Densité spectrale d'énergie d'Einstein
En égalisant les densités spectrales d'énergie d'Einstein et de Planck (Equation 9 et Equation 16), il vient :
Rho (Nu) = (8 * pi * Nu² / c3) * h * Nu / (exp (Beta * h * Nu) - 1) = A21 / ((exp(h * Nu / (k * T)) - 1) * B21)
D'où :
A21 / B21 = (8 * pi * Nu² / c3) * h * Nu, et
A21 / B21 = 8 * pi * h / Lambda3
Equation 17 Rapport A/B d'Einstein
Bilan :
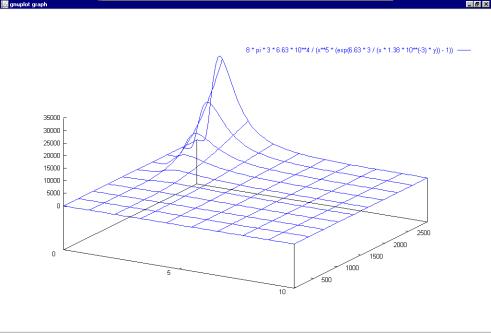
Figure 12 Loi du corps noir de Planck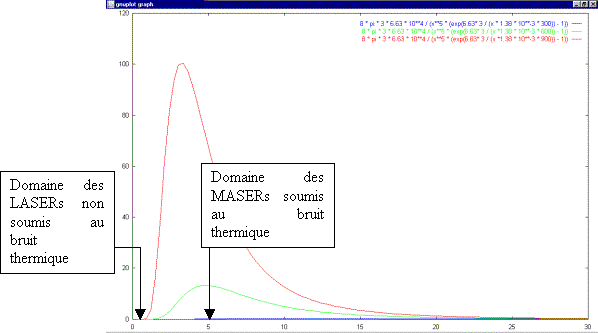
Figure 13 Déplacement de Wien avec la loi du corps noir de Planck
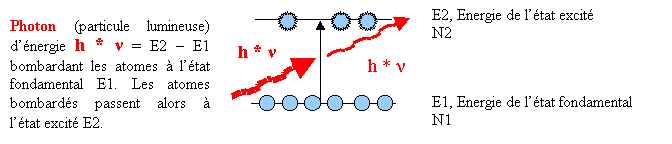
Figure 14 Absorption d'un photon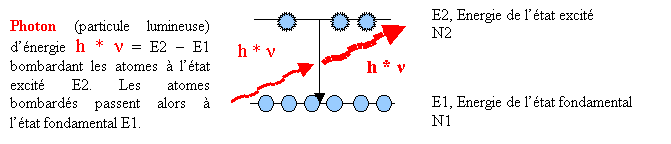
Figure 15 Emission stimulée d'un photon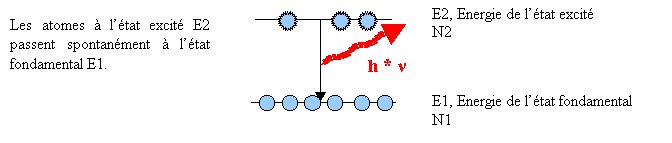
Figure 16 Emission spontanée d'un photon
(c) On line since february 2002 - Do not make any copy of this document witout prior written approval.