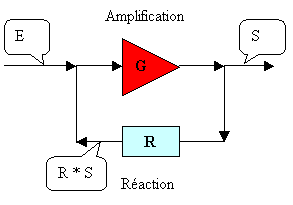
Figure 1 Amplificateur électronique
En électronique classique, un amplificateur à électrons (de type amplificateur opérationnel, ou " ampli op ", par exemple), est caractérisé par :
· Une tension d'entrée E
· Une tension de sortie S
· Un gain en tension (ou en intensité) G tel que :
o S = G * E sans réaction (R = 0)
o S = G * (E + R * S) = (G / (1 - G * R)) *E avec réaction (R différent de 0)
· Un gain effectif Geff = G / (1 - G * R) dans le cas d'une réaction
· Un coefficient de réaction R :
o Si 0 < R < 1 alors il y a réaction et Geff > G
o Si -1 < R < 0 alors il y a contre-réaction et Geff < G
o Si G * R >= 1 alors il y a oscillation et Geff tend vers l'infini. La relation précédente est appelée condition d'oscillation.
Le seuil d'oscillation est défini lorsque :
G * R = 1
Equation 2 Condition d'oscillation d'un amplificateur

Figure 1 Amplificateur électronique
En optique, il ne faut plus raisonner avec des électrons (particule appartenant à la famille des fermions) comme en électronique mais avec des photons (particule appartenant à la famille des bosons). Un amplificateur optique est caractérisé par :
· Une intensité d'entrée Io ;
· Une intensité de sortie Is ;
· Un milieu actif :
o de gain optique G = Is / Io avec Is = Io exp (Alphao * L),
o de longueur L ;
o de gain par unité de longueur Alphao strictement positif (dans le cas contraire, il s'agirait d'un coefficient d'absorption linéique)
· Une réaction optique obtenue à l'aide de miroir semi-réfléchissants de pouvoir réflecteur en intensité R. La condition d'oscillation étant respectée :
o G * R >= 1 d'où
o R * exp (Alphao * L) >= 1 et
o Alphao * L >= - ln R > 0 donc
o 0 < R < 1 est bien respecté (un pouvoir réflecteur est compris entre 0 et 100 %)
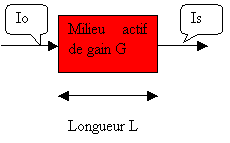
Figure 2 Amplification optique
Il existe deux types de cavités LASER :
· LASER en anneau pour lequel les pouvoirs réflecteurs des 3 surfaces réfléchissantes rencontrées par le faisceau LASER sont multipliés entre eux : G * R1 * R2 * R3 >= 1
· LASER à Fabry-Perot pour lequel les pouvoirs réflecteurs des 2 surfaces réfléchissantes rencontrées par le faisceau LASER sont multipliés entre eux ainsi que les gains du milieu actif deux fois traversé : G * R1 * G * R2 >= 1
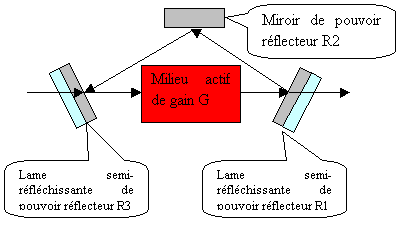
Figure 3 LASER en anneau

Figure 4 LASER à cavité Fabry-Perot
3.1.2. Classification des LASERs
Les LASERs sont caractérisés par :
§ leur régime de fonctionnement :
o continu
o pulsé : la puissance crête est atteinte durant un très court instant, avec une fréquence de l'ordre du GHz. Ce type de LASER est également appelé " LASER nano-seconde ".
§ la nature de leur milieu actif :
o gaz, excimère ou vapeur de métal ;
o solide de type rubis (Cr3+), YAG (Nd3+), semi-conducteur ou isolant ;
o Liquide de type colorants ;
o A électrons libres nécessitant un accélérateur d'électrons.
§ leur rendement, défini par le rapport de la puissance utile (lumière émise) sur la puissance fournie (électricité consommée) :
o 10-4 pour le LASER à Argon ;
o 20 % pour le LASER à CO2 utilisé dans l'industrie pour les soudures (ce qui est moins onéreux que l'étain traditionnellement utilisé) ;
o 70 % pour le LASER à semi-conducteur à basse température.
3.1.3. LASERs à gaz
Les LASERs à gaz de type He-Ar et He-Ne sont apparus en 1960 et 1962 respectivement et possèdent une réaction R élevée et un faible gain G. Ils sont composés d'une ampoule de verre contenant le milieu actif (le gaz) dans lequel il est possible d'appliquer une décharge électrique. Afin de limiter les pertes au niveau des surfaces de verre traversées par le faisceau lumineux, des fenêtres de Brewster sont utilisées. En effet, un faisceau lumineux dont l'angle d'incidence i avec une lame de verre vérifie la relation d'optique tan i = n avec n, l'indice de réfraction du milieu traversé (le verre) et i l'angle dit de Brewster, sera transmis totalement. Cette enceinte de gaz est placée entre les deux lames semi-réfléchissantes d'une cavité Fabry-Pérot. Le pouvoir réflecteur est égal au produit des pouvoirs réflecteurs des deux miroirs : R = R1 * R2.
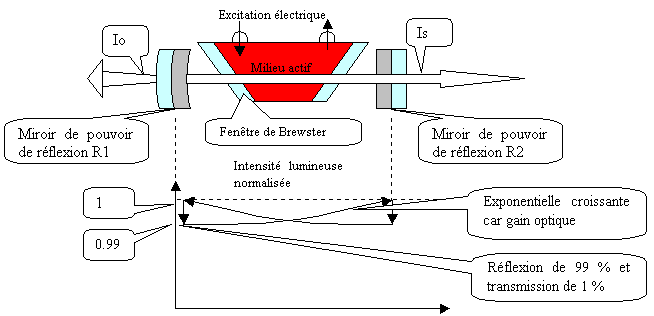
Figure 5 Principe d'un LASER à gaz
Les miroirs suivant la loi de conservation de l'énergie qui dit que la somme des pouvoirs réflecteur R, de transmission T, d'absorption A et de diffusion D est égale à 1, nous en déduisons, en l'absence de diffusion et absorption que le pouvoir de réflexion R = 1 - T. Donc pour R élevé et T faible :
§ Alphao * L >= - ln R devient
§ Alphao * L >= - ln (1 - T) et comme T est petit devant 1, le développement limité ln (1 + x) # x peut être appliqué et
§ Alphao * L >= T.
Pour un LASER à He-Ne, R = 99 % donc T = 1 % et le gain G satisfait :
§ G = exp (Alphao * L) >= exp T et comme T est petit devant 1, le développement limité exp x # 1 + x peut être appliqué et
§ G >= 1 + T = 1.01
C'est-à-dire que lorsque le faisceau incident traverse la cavité, son gain est de l'ordre de 1 % et pour cette raison, un LASER à gaz est dit à faibles gain.
3.1.4. LASERs à semi-conducteur
Les LASERs à semi-conducteur sont apparus en 1962 et possèdent une faible réaction R et un gain G élevé. Le milieu actif forme une couche d'indice de réfraction n = 3.5 dans le cas du GaAs (Arséniure de Gallium). Cette couche est prise en sandwich entre deux autres couches d'indice de réfraction différent de sorte que la couche correspondant au milieu actif fasse office de guide d'onde. Ces trois couches forment un parallélépipède plongé dans l'air d'indice de réfraction n = 1 si bien que deux des faces de ce parallélépipède forment naturellement les deux miroirs de la cavité Fabry-Pérot.
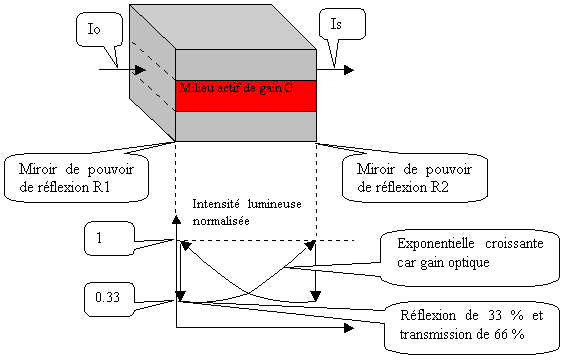
Figure 6 Principe d'un LASER à semi-conducteur
Lorsque le faisceau d'intensité entrante Io est perpendiculaire au miroir (incidence normale), le pouvoir réflecteur est, d'après les lois de l'optique, R = ((n - 1) / (n + 1))² = 0.3 pour n = 3.5 donc, pour vérifier la condition d'oscillation G * R >= 1, il faut que le gain G >= 3.3 et c'est la raison pour laquelle un LASER à semi-conducteur est dit à fort gain.