Figure 36 LASER à SC (diode LASER) observé au microscope
4.3. Etude des propriétés des LASERs à SC
4.3.1. LASERs à SC étudiés
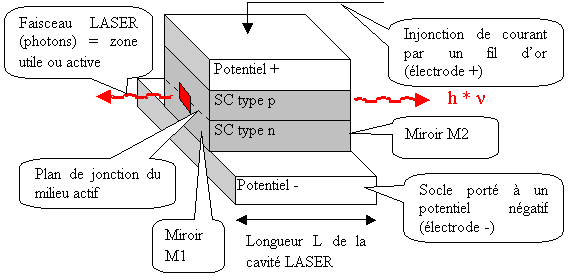
Etudions un LASER solide à base de SC (InGaAsP) ainsi qu'un LASER à émission de surface (VCSEL composé de AlGaAs). Un LASER à SC, observé au microscope possède l'allure suivante :

Figure 36 LASER à SC (diode LASER) observé au microscope
Le SC ci-dessus est encapsulé dans une enceinte sous ultra-vide et constitue une diode LASER. L'indice de réfraction du SC utilisé est n = 3.5 d'où le pouvoir de réflexion des miroirs M1 et M2 (constituant les interfaces entre le SC et l'ultra-vide qui l'entoure) R = ((n - 1)/(n + 1))² # 0.3 et le gain seuil d'une telle cavité G = 1 / R # 3 (d'après la condition de seuil d'oscillation). La longueur de la zone active est L = 367 µm.
Notons que dans le cas d'un LASER à gaz de type He-Ne fonctionnant dans l'infrarouge à la longueur d'onde de 3.39 µm et dont la cavité possède une longueur L = 40 cm, le gain seuil est G # 1.5. Si bien que le rapport encombrement / gain d'un LASER à SC est très faible, d'autant plus que le prix d'une diode LASER est d'environ 15 €. C'est la raison pour laquelle les LASERs à SC sont aujourd'hui largement employés dans les lecteurs d'étiquettes, les lecteurs de disque compact (CD) et dans les stylos-pointeur par exemple.
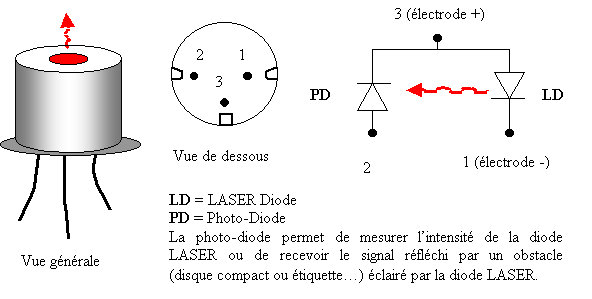
Figure 37 Descriptif d'une diode LASER
Le bloc LASER de cette étude comprend quatre éléments essentiels reliés par des contacts isolés par un corps gras spécial :
Ces quatre éléments sont reliés à un bloc de régulation permettant de faire varier :
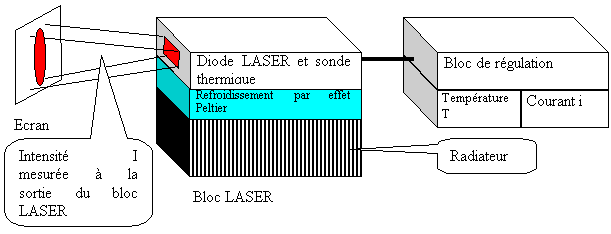
Figure 38 Dispositif expérimental de l'étude
4.3.2. Gain d'un LASER à SC
Nous avons vu que le gain linéique g(Nu) d'un LASER dépendait de la fréquence Nu. Le gain dépend également de la longueur L de la cavité LASER. Notons G (Nu, L) ce nouveau gain, qui s'exprime en fonction du précédent de la manière suivante :
G = G (Nu, L) = exp (g(Nu) * L)
Equation 24 Gain d'un LASER
Au seuil d'oscillation, G * R = 1 donc exp (gseuil * L) * R = 1
C'est-à-dire que le gain linéique possède l'expression suivante au seuil d'oscillation :
gseuil = - (1 / L) * ln R
Equation 25 Gain linéique du LASER au seuil d'oscillation
Au seuil d'oscillation, le gain linéique est égal aux pertes (par réflexion) par unité de longueur de la cavité LASER. Pour R = 30 %, n = 3.5 et L # 300 µm alors gseuil # 40 cm-1 ce qui correspond à Gseuil # 3.
Par injection d'un courant i dans le SC et pour une excitation des modes d'oscillation (le seuil d'oscillation est dépassé), alors nous observons :
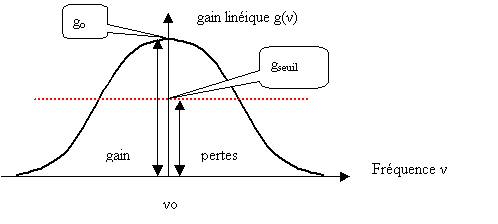
Figure 39 Gain linéique g(Nu) d'un LASER et gain seuil gseuil
En régime non-stationnaire, le gain go est supérieur au seuil gseuil. Le seuil d'oscillation est dépassé et l'intensité du LASER, sans cesse amplifiée, diverge.
Le système fonctionne en régime stationnaire si après un aller-retour dans la cavité LASER (le milieu actif est traversé deux fois et est réfléchi par les deux miroirs M1 et M2) le système se retrouve dans le même état et possède la même intensité de sortie I du LASER (mesurée avec un photo-détecteur placé à la place de l'écran). Pour atteindre ce régime, il est nécessaire de saturer le gain gs au niveau des pertes (correspondant au gain seuil gseuil) en réutilisant le gain en excès (sous forme d'intensité de sortie) :
gs = go / (1 + I / Is)
Equation 26 Gain linéique saturé (au niveau des pertes)
Avec :
Nous en déduisons donc :
I = Is * (go / gseuil - 1)
I = Is * ((go - gseuil) / gseuil)
I = Is * ((go + (1 / L) * ln R) / (- (1 / L) * ln R))
I = Is * ((go - pertes) / pertes) avec pertes = gseuil = - (1 / L) * ln R
Equation 27 Intensité de sortie du bloc LASER
4.3.3. Puissance de sortie
La puissance de sortie Ps du bloc LASER est proportionnelle à l'intensité de sortie I tout comme le gain linéique go est proportionnel au courant i injecté dans la diode LASER. Au cours de cette étude, nous avons mesuré la puissance de sortie Ps en fonction du courant d'injection i ( et donc du gain linéique go) pour différentes températures de régulation T. Pour cela, et le faisceau LASER étant suffisamment large, le photo-détecteur et plaqué directement à la sortie de la diode LASER.
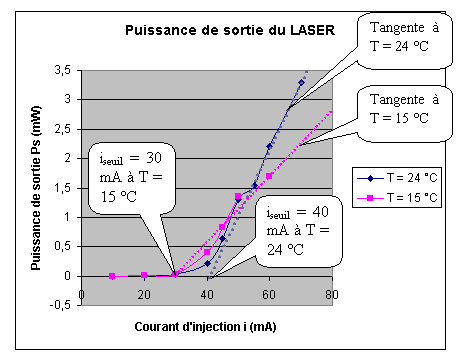
Figure 40 Puissance de sortie du LASER en fonction du courant d'injection et de la température de régulation
Le courant d'injection de seuil iseuil est déterminé grâce à la tangente de la courbe Ps (i) et celui-ci décroît lorsque la température de régulation T augmente. Le constructeur de la diode LASER donne un courant de seuil dans l'intervalle 40 à 60 mA et ne fournit la courbe Ps (i) que jusqu'à 60 mA car au-delà, des modes d'oscillation tranverses sont excités (en plus des modes longitudinaux de la cavité LASER de longueur L) et des " accidents " de courbe apparaissent. Pour utiliser de faibles courants de seuil, la diode LASER doit être utilisée à basse température, d'où l'intérêt du système de refroidissement par effet Peltier.
L'efficacité quantique différentielle (EQD) est définie comme le rapport de la variation de puissance de sortie / variation de courant d'injection pour i > iseuil ce qui correspond à la pente de la tangente. Dans notre étude :
Généralement, les constructeurs de diodes LASER, peu scrupuleux, préfèrent fournir l'efficacité quantique différentielle plutôt que le rendement lumineux qui est inférieur. Comme toute diode, la diode LASER possède une tension de seuil Vd au-dessus de laquelle la diode est " passante " et en dessous de laquelle la diode est " bloquée ". La caractéristique de la diode possède l'allure suivante :
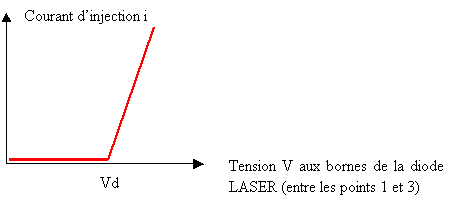
Figure 41 Caractéristique d'une diode (LASER)
D'après le constructeur, la tension seuil Vd est de 2 Volts. Le rendement lumineux s'en déduit :
Rendement Lumineux = Psmax / Pc = Psmax / (Vd * iseuil)
Equation 28 Rendement Lumineux de la diode LASER
Avec :
Dans notre étude :
Le rendement d'un LASER à SC est faible mais supérieur à un LASER à gaz de type Argon qui n'est que d'environ 0.01 % à cause du système de refroidissement qui consomme énormément d'énergie.
Bilan :
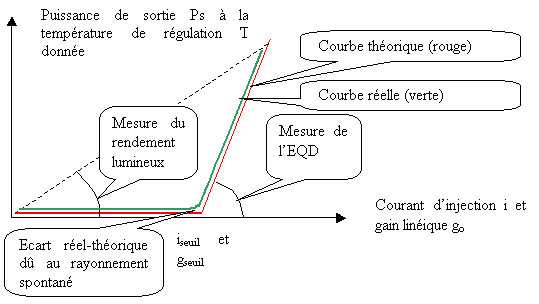
Figure 42 Synthèse sur la courbe Ps (i)
4.3.4. Diagramme de rayonnement
La zone utile ou active du SC possède une largeur de :
Ces deux largeurs se déduisent des divergences perpendiculaire Tetaperp et parallèle Tetapara du faisceau LASER, dont la longueur d'onde est de 0.67 µm. Ces largeurs ou " waists " (d'où le " W " dans leurs expressions) sont de l'ordre du micromètre :
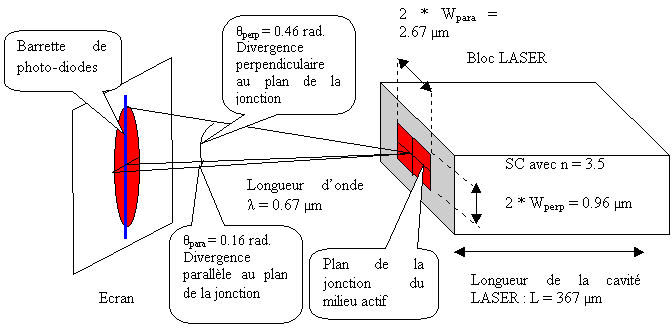
Figure 43 Dispositif de mesure du faisceau LASER
Pour analyser le faisceau LASER, nous n'utilisons pas un simple écran mais plutôt une barrette de photodiodes (comme dans les caméras CCD) que nous placerons parallèlement ou perpendiculairement au plan de jonction du milieu actif. La barrette comporte 1024 diodes (1024 pixels) séparées de 25 µm, d'où la largeur de la barrette de 25.6 mm. La barrette est placée à 14 millimètres du miroir M1 et un filtre de 5 millimètres d'épaisseur est interposé afin de ne pas dégrader la barrette de photo-diodes. La température de régulation est fixée à T = 15 °C et le courant d'injection (d'excitation) est i = 50 mA.
En plaçant la barrette de diode parallèlement au plan de la jonction du milieu actif (pas comme sur la figure ci-dessus), nous pouvons analyser le profil du faisceau LASER dans le plan (horizontal) de la jonction. Le signal lumineux reçu par la barrette de photo-diodes est observé sur l'écran d'un oscilloscope.
Un profil Gaussien est obtenu, dont la largeur à 1/e² = 13,5 % (avec e = exp 1 = 2.73) de la hauteur donne la divergence horizontale du faisceau LASER Gaussien :
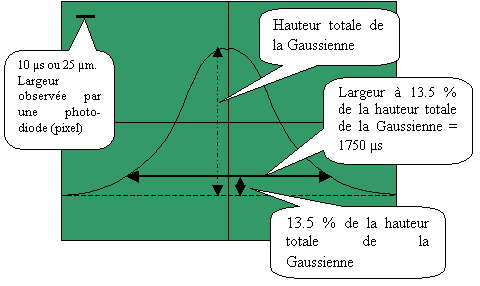
Figure 44 Profil Gaussien du faisceau LASER observé dans le plan de la jonction
Notons que la largeur associée à une photo-diode est balayée en 10 µs par l'oscilloscope d'où l'association largeur-temps. La largeur de la Gaussienne à 13.5 % de sa hauteur est de 1750 µs à 14 mm de la sortie de la diode LASER, soit une largeur de faisceau LASER de 1750 µs * 25 µm / 10 µs = 4.4 mm. D'où la divergence horizontale ou parallèle du faisceau LASER :
Tetapara = arctan (4.4 / (2 * 14)) = 9.9 ° = 0.16 rad
De la même manière, après avoir fait pivoter la barrette de photo-diodes de 90 °, nous obtenons la divergence verticale ou perpendiculaire du faisceau LASER, toujours Gaussien :
Tetaperp = 26.6 ° = 0.46 rad
Les largeurs du milieu actif du SC s'en déduisent immédiatement connaissant la longueur d'onde d'émission du LASER à SC qui est de 0.67 µm :
Bilan :
4.3.5. Espacement entre modes successifs
Le gain linéique g (Nu) en sortie du LASER dépend de la fréquence (et donc de la longueur d'onde si bien que nous pouvons le noter g (Lambda) également) et possède une allure Gaussienne centrée autour de la longueur d'onde Lambda = 0.67 µm = 670 µm. Toutefois, la courbe de gain linéique n'est que l'enveloppe d'un spectre de raies. La courbe précédente représentant le spectre des modes de la cavité LASER est obtenue à l'aide d'un monochromateur placé en sortie du LASER.
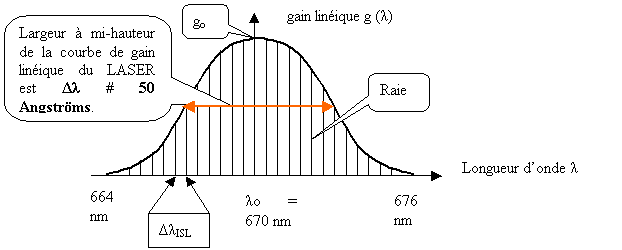
Figure 45 Profil de raies du gain linéique
A chaque raie correspond un mode d'oscillation de la cavité LASER (comme les harmoniques d'une guitare correspondent aux différents modes d'oscillation de la corde). Contrairement à l'enveloppe Gaussienne, les raies ont individuellement un profil Lorentzien. L'intervalle séparant deux raies s'appelle intervalle spectral libre (ISL) et dépend de la longueur L de la cavité LASER. Cet intervalle s'exprime en fréquence (deltaNuISL) ou en longueur d'onde (deltaLambdaISL) ;
L = c / (2 * n * deltaNuISL) = Lambdao² / (2 * n * deltaLambdaISL)
Equation 29 Longueur de la cavité LASER en fonction de l'intervalle spectral libre (ISL)
Avec :
Dans cette étude, la longueur L = 367 µm de la cavité LASER a été obtenue en mesurant deltaLambdaISL pour différentes valeurs du courant d'injection i. Quel que soit i, la longueur de la cavité L est constante. Toutefois, lorsque le courant d'excitation (ou d'injection) i augmente, la Gaussienne décrivant le gain linéique de la cavité devient de plus en plus aigu et sa largeur à mi-hauteur diminue. L'ISL mesuré entre deux modes longitudinaux (ou raies) successifs est deltaLambdaISL = 0.175 nm # 2 Angströms, ce qui correspond à deltaNuISL = 130 GHz car deltaLambdaISL / Lambda = deltaNuISL / Nu. Cette valeur est suffisamment élevée pour qu'un simple monochromateur suffise à observer les modes longitudinaux. Par contre, dans le cas d'un LASER à gaz à base de He-Ne, de longueur L = 300 mm, l'ISL est de l'ordre de 500 MHz, ce qui est trop faible pour observer les modes et une cavité Fabry-Pérot est alors nécessaire.
Bilan :
4.3.6. Polarisation
La lumière possède une nature ondulatoire. En effet, elle est créée par la propagation de champs (électriques E et magnétiques H) orientés perpendiculaires à la direction de propagation de la lumière (figurée par le vecteur d'onde k). L'amplitude des champs électriques et magnétiques varie de façon sinusoïdale. La longueur d'onde du faisceau lumineux correspond à la période spatiale avec laquelle l'amplitude revient à son état initial.
La polarisation de l'onde lumineuse est caractérisée par le vecteur champs électrique E. Celle-ci est orientée parallèlement au plan de la jonction du SC (par analogie aux guides d'onde, la polarisation est alors dite de type TE = Transverse Electric) ou perpendiculairement au plan de la jonction du SC (la polarisation est alors dite de type TM = Transverse Magnetic).
A l'intérieur de la cavité formée par les différences d'indice de réfraction du SC, les pouvoirs de réflexion des faces ne sont pas les mêmes. Selon les deux directions (parallèle ou perpendiculaire au plan de la jonction du SC), les pouvoirs de réflexion des faces du SC (guide d'onde) sont RTE # 0.3 et RTM #0.27. Plus le pouvoir de réflexion est grand dans une direction, plus la lumière est réfléchie et donc correctement guidée, ce qui est l'objectif du guide d'onde. La polarisation est maximale dans le mode TE, c'est-à-dire parallèlement à la jonction.
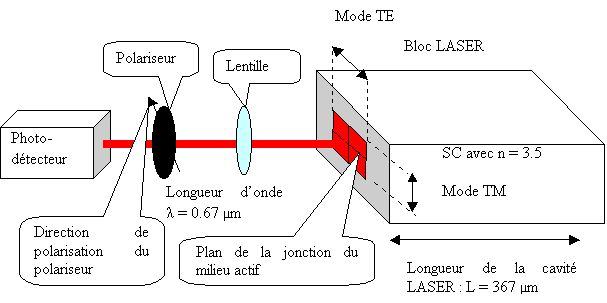
Figure 46 Polarisation du faisceau LASER
A l'aide d'un polariseur, ne laissons passer que la composante du vecteur champs électrique E du faisceau LASER, parallèle à la direction de polarisation du faisceau LASER. Le faisceau LASER ne traversera le polariseur que si son champs électrique est orienté dans la direction de polarisation du polariseur. Dans cette étude, faisons varier la direction de polarisation au niveau du polariseur et mesurons l'intensité I du faisceau LASER transmise au photo-détecteur. Si le LASER est polarisé en mode TE, le signal sera maximal lorsque la direction de polarisation du polariseur sera réglée de manière parallèle au plan de la jonction du milieu actif du SC.
Le taux de polarisation d'un LASER est obtenu en faisant varier la direction de polarisation entre 0 et 360°. L'intensité maximale mesurée est Imax et l'intensité minimale mesurée est Imin et le taux de polarisation du LASER est défini par :
Tx-pol = Imax / Imin
Equation 30 Taux de polarisation Tx-pol d'un faisceau LASER
Le taux de polarisation dépend du courant d'excitation (ou d'injection) i du milieu actif :
| Courant d'excitation i (mA) | 50 | 30 = iseuil |
| Imin (Volt) | 0.9 | 1 |
| Imax (Volt) | 121 | 10 |
| Tx-pol | 134 | 10 |
Table 2 Mesure du taux de polarisation du LASER à T = 15 °C
Plus le courant d'excitation augmente (s'écarte du courant de seuil), plus le taux de polarisation augmente et plus la polarisation devient horizontale (mode TE favorisé). Ceci s'explique par le rapport bruit/signal = spontané/stimulé = A21 / (B21 * i). Plus i augmente, plus ce rapport diminue et plus le signal ou rayonnement stimulé l'emporte sur le bruit ou rayonnement spontané. L'augmentation de la part de stimulé (dû à l'inversion de population rappelons-le) a pour conséquence l'apparition de la polarisation horizontale. Le spontané est associé à une polarisation isotrope (dans toutes les directions) alors que le stimulé favorise une direction de polarisation. Pour i élevé, le spontané ne perturbe plus le stimulé et la polarisation du signal apparaît franchement (polarisation rectiligne parallèle au plan de la jonction).
Notons que pour les LASERs à gaz de type Argon, le taux de polarisation diminue lorsque le courant d'excitation augmente et ceci à cause de l'augmentation de l'effet Zeeman (séparation des niveaux d'énergie atomiques en sous-niveaux d'énergie dégénérés).
4.3.7. Réseaux de diodes LASER (Arrays)
Le milieu actif du LASER à SC précédent possède un volume de 0.96 * 2.67 * 367 = 941 µm3 et contient 1018 atomes par cm3 donc il est possible d'implanter plusieurs LASERs côte à côte et de les superposer sur une même plaque de SC à base de GaAs.
Deux applications en résultent :
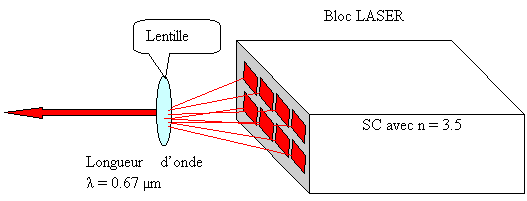
Figure 47 Application des réseaux de diodes LASER à la forte puissance
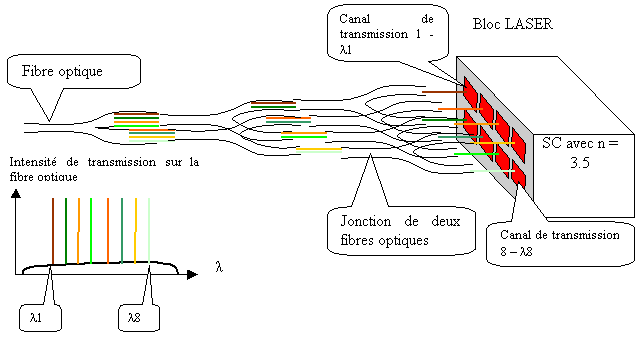
Figure 48 Application des réseaux de diodes LASER aux télécommunications (WDM)
4.3.8. LASERs monomodes
Un LASER est dit monomode si la cavité qui le compose ne possède qu'un seul mode d'oscillation possible. Nous avons vu que pour un LASER dont la cavité avait pour longueur L = 367 µm, 25 modes d'oscillation s'établissaient. Cherchons à réduire ce nombre à un seul mode. Pour cela, il sexiste plusieurs solutions appelées LASERs monomodes :
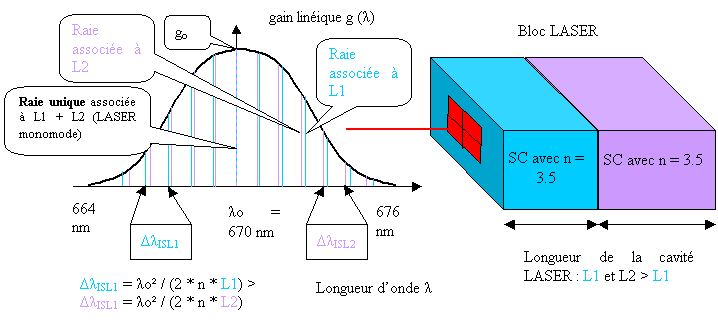
Figure 49 Principe d'un LASER C3 (Coupled Clived Crystal)
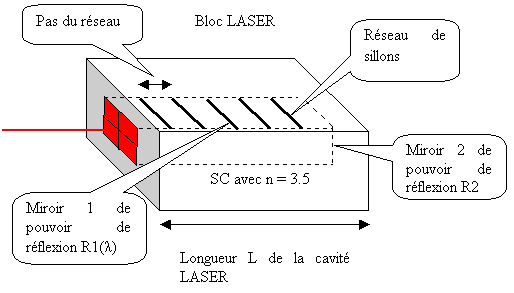
Figure 50 Principe d'un LASER DFB (Distributed FeedBack)
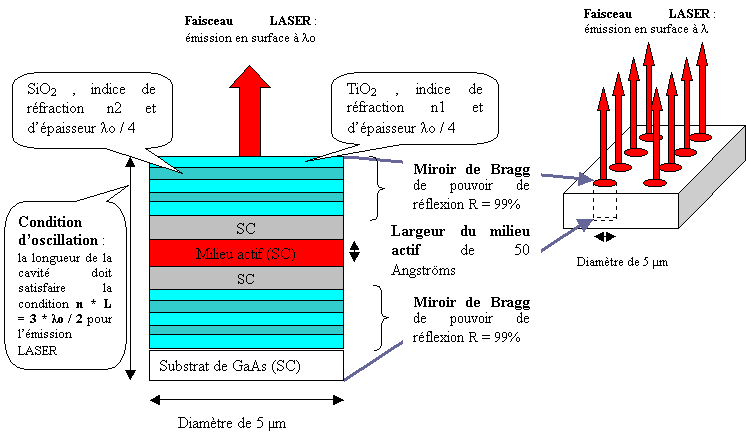
Figure 51 Principe d'un LASER VCSEL
Notons que pour construire un miroir de Bragg, il est nécessaire d'empiler 20 couches alternativement de TiO2 et SiO2 pour leurs indices de réfraction différents n1 et n2 respectivement. Ces couches ont pour épaisseur Lambdao / 4 et permettent d'atteindre un pouvoir de réflexion de 98 à 99 %.
La condition de gain G * R = 1 donne, pour R = 98 %, G = 1.02 ce qui est suffisant pour faire osciller le LASER à la fréquence Nuo = 3.53 * 1014 Hz, soit une longueur d'onde Lambdao = c / Nuo = 0.850 µm (domaine infrarouge). L'intervalle spectral libre est donc deltaNuISL = c / (2 * n * L) = c / (3 * Lambdao) = Nuo / 3 = 1.18 * 1014 Hz en prenant en compte la condition d'oscillation.
Comme la largeur à mi-hauteur de la courbe de gain d'un LASER à SC est deltaLambda # 50 Angströms, ce qui correspond à deltaNu # 2 * 1012 Hz pour Lambdao = 0.850 µm alors le VCSEL est un LASER monomode de par sa structure.
De plus, à T = 21 °C, un courant de seuil iseuil = 1.79 mA est nécessaire. Ce courant de seuil est inférieur à celui d'une diode LASER.
Pour un courant d'injection i = 10 mA et une tension de diode Vd = 1.6 Volt, la puissance de sortie d'un tel LASER est Ps = 0.461 mW d'où un rendement lumineux de 2.9 %, supérieur à celui de la diode LASER.
Il est possible de créer un réseau de LASERs de type VCSEL, comme le montre la figure précédente, à condition que le diamètre du LASER soit suffisamment faible pour que des modes obliques d'oscillation n'apparaissent pas. L'application d'un tel réseau au multiplexage en longueur d'onde WDM est facilement imaginable (Figure 48 et Figure 51).
Bilan :